When Instrumental Variable (IV) is problematic

As a tutor for both Australia Awards Scholarship and ANU, I get the privilege to learn many courses. There’s a lot of great content in ANU in terms of courses which I can’t cope with. But as a tutor, I am ‘forced’ to learn many of these courses so that’s definitely something. Haha!

This time, i’d like to write about a demonstration of weak instrument that I learned from a course at CBE.

What’s an IV?

One problem with OLS is endogeneity/reverse causality. This happens when our independent variable is actually depending on something else. This something else is then absorbed by the error term and violate $E[MXM\epsilon] \neq 0$.

We often use IV as one of the treatment to this problem. IV is a third variable $Z$ that should be independent from $Y$ but have high correlation with $X$. IV will establish $X$ causes $Y$ but not $Y$ causes $X$.

Problem IV

However, when the instrument $Z$ is not explaining $X$ very well, IV may lead to even more bias. We try to simulate this using R below.

Setting

Here, we try to use finance setting. Let $X$ be a firm’s cash flow while $Y$ is firm’s borrowing. We try to establish causal relationship between $X$ and $Y$. When firm’s cash flow is negative, it will need to borrow from financial market to survive for the next revenue collection time. However, when firm’s cash flow is positive, it may also borrow if the positive cash flow is a sign of positive shock and the firm needs fund to expand. We can use technological shock $Z$ as an instrument for $X$.

Generate 2,000 observation, where half experienced a flat negative shock $( − 3 + rand())$ while half experience positive shock $X = Z + rand()$.

data <- data.frame(
  id=c(1:2000)
)

# generate data observation
data$lnz <- rnorm(2000, mean = 0.5, sd=1)
data$Z <- exp(data$lnz)
data$U <- rnorm(2000,mean = 0, sd=0.1)
data$B1 <- rbinom (2000, 1, 0.5)  # to explain about probability 1
data$B2 <- 1-data$B1  # to explain about probability 1

# generate firm cashflow
data$X <- data$B1*data$Z - 3*data$B2 + data$U

# generate firm borrowing
data$E <- rnorm(2000,mean = 0, sd=0.1)
data$R <- 0.5*data$U + 0.5*data$E
data$X1 <- ifelse (data$X>0, 1, 0)
data$X2 <- ifelse (data$X<0, 1, 0)
data$Y <- (data$X*data$X1) - (data$X*data$X2) + data$R
head(data)

##   id         lnz         Z           U B1 B2         X           E           R
## 1  1  0.53446900 1.7065418 -0.02069438  1  0  1.685847 -0.16523761 -0.09296600
## 2  2 -0.25843412 0.7722599 -0.01968836  0  1 -3.019688 -0.09326667 -0.05647752
## 3  3  0.58658233 1.7978335  0.05513357  0  1 -2.944866 -0.10034947 -0.02260795
## 4  4  1.48663543 4.4221917 -0.18736333  0  1 -3.187363 -0.10648732 -0.14692532
## 5  5  1.07463211 2.9289152  0.04403934  0  1 -2.955961  0.03063488  0.03733711
## 6  6  0.05710789 1.0587700  0.03335503  1  0  1.092125  0.07427162  0.05381333
##   X1 X2        Y
## 1  1  0 1.592881
## 2  0  1 2.963211
## 3  0  1 2.922258
## 4  0  1 3.040438
## 5  0  1 2.993298
## 6  1  0 1.145938

Positive cash flow $X$ have a 1-on-1 relationship with positive $Z$, but a flat $-3$ with negative $Z$.

Let’s try plot $Z$ and $X$

library(ggplot2)
a<-ggplot(data, aes(Z,X, colour=B1)) +
    geom_point()
a

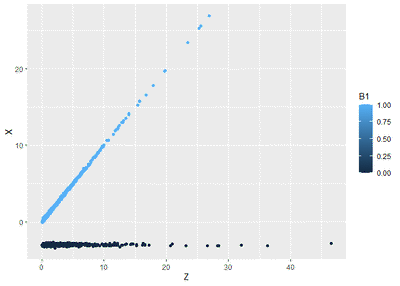
Blue is those experience positive shock while black is those who get negative shock. Positive shock has 45^∘ from $X = 0$ while all the negative ones are flat around $X = -3$. Look at that. What a bad pattern. Horrible for researchers 🤣🤣.

Now let’s try $X$ and $Y$:

b<-ggplot(data,aes(X,Y,colour=X1)) +
  geom_point()
b

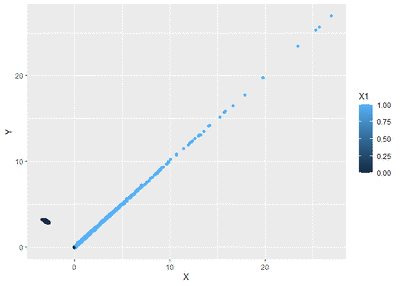
Firm’s borrowing sudah pasti positif, dan kita buat sedemikian sehingga perusahaan meminjam sesuai cash flow (alias koefisien beta-nya = 1). Nah, ketika $X$ =  − 3, mereka minjamnya $Y$ = 3, makanya yang hitam ngumpul di ($X$, $Y$) = ( − 3, 3) semua, sementara yang biru punya tren lurus dengan sudut 45^∘ alias $Y$ = $X$.

Jika kita, ceritanya nggak tau hubungan $X$, $Y$ dan $Z$ di dunia nyata, meregresikan $X$ dan $Y$ dengan OLS biasa, kira-kira seperti apa bentuknya?

b +
  geom_smooth(method = "lm")

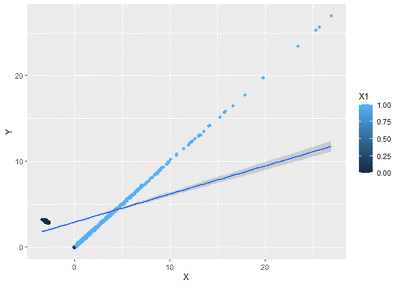
Keliatan bias banget yah?

Bagaimana dengan koefisiennya? Coba anda bisa nebak gak? ingat bahwa ketika $X$ positif, $X$ naik 1 beriringan dengan $Y$ naik sebanyak 1, sementara ketika $X$ negatif, $X$ turun 1 beriringan dengan $Y$ naik 1 juga. Sementara itu ada 50% $X$ yang negatif, dan 50% $X$ yang positif. Jika kita regresi biasa, kira-kira koefisiennya berapa? Coba tebak!

# Regression
mod <- lm(Y~X, data = data)
summary(mod)

## 
## Call:
## lm(formula = Y ~ X, data = data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.0007 -1.7264  0.9776  1.1259 15.2347 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.88313    0.04075   70.76   <2e-16 ***
## X            0.32862    0.01145   28.70   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.82 on 1998 degrees of freedom
## Multiple R-squared:  0.2919, Adjusted R-squared:  0.2916 
## F-statistic: 823.7 on 1 and 1998 DF,  p-value: < 2.2e-16

Jawabannya (hampir) benar! (hampir) 0.5! Jadi sebenarnya dengan OLS, kita sudah mendapatkan koefisien yang (hampir) sesuai dengan data yang kita regenerasi, yaitu (hampir) 0.5! Yah tentu saja hasilnya masih salah wkwkwk karena 0.32 masih agak jauh dari 0.5 yha, tapi kan ceritanya kita gak tau dunia nyata bentuknya kayak gimana he he he.

Regresi IV malah bikin tambah jelek

Tentu saja OLS belum ngasih kita koefisien yang kita inginkan ya (tentu saja masalah bias masih ada). Yang jadi masalah, regresi IV malah bikin koefisiennya makin menjauh dari 0.5!

Coba kita regresi $Y$ dan $X$ dengan menggunakan $Z$ sebagai instrumen:

library (AER)

modelIV <- ivreg(formula=data$Y~data$X | data$Z)
summary(modelIV)

## 
## Call:
## ivreg(formula = data$Y ~ data$X | data$Z)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -5.366 -3.175 -2.877  3.252  3.884 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.01206    0.07358   40.94   <2e-16 ***
## data$X       1.08897    0.05915   18.41   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.26 on 1998 degrees of freedom
## Multiple R-Squared: -1.271,  Adjusted R-squared: -1.272 
## Wald test:   339 on 1 and 1998 DF,  p-value: < 2.2e-16

Setelah di-treat dengan IV, koefisien X dan Y malah bermasalah. Tapi sebenernya kan memang kita meregresikan X dan Y dengan koefisien 1 (meskipun aslinya 50% doang, 50%-nya lagi koefisien -1) Tentu saja, IV-nya hanya menangkap 50% dari fenomena, dan 50%-nya lagi akhirnya diserahkan ke intercept (dan error). OLS emang masih ada bias, tapi IV malah bikin tambah parah. Inilah salah satu contoh problem menggunakan IV, jika hubungan IV nya sendiri bias.

Cara terbaik? Tentu saja memisahkan regresinya jadi dua. Contoh jika kita regresi hanya shock positif saja:

dataX<-data
dataX<-dataX[!(dataX$B2=="1"),]

modelIV2 <- ivreg(formula=dataX$Y~dataX$X | dataX$Z)
summary(modelIV2)

## 
## Call:
## ivreg(formula = dataX$Y ~ dataX$X | dataX$Z)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.228315 -0.047317  0.002166  0.045417  0.201270 
## 
## Coefficients:
##              Estimate Std. Error  t value Pr(>|t|)    
## (Intercept) 0.0020950  0.0028174    0.744    0.457    
## dataX$X     0.9997967  0.0006977 1432.905   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.06716 on 999 degrees of freedom
## Multiple R-Squared: 0.9995,  Adjusted R-squared: 0.9995 
## Wald test: 2.053e+06 on 1 and 999 DF,  p-value: < 2.2e-16

Ini benar. Intercept = 0, dan koefisiennya 1, sesuai dengan yang kita buat. Tentu saja yang negatif tidak perlu kita IV karena ketika negatif, $X$ akan otomatis -3. Artinya, untuk yang negatif, $X$ sudah eksogen! Tidak perlu ditreatment apa-apa (meskipun, coba lihat bagaimana saya generate error term?)

Intinya, hati-hati menggunakan IV

Tentu saja di dunia nyata kita tidak tau fungsi asli dari $Y=f(X)$, dan biasanya memang IV kita gunakan untuk memperbaiki kelemahan OLS. Sayangnya IV dapat berbahaya jika instrumennya tidak menjelaskan dengan baik penyebaran dari variabel endogen yang di-treat, atau jika anda tidak tau-tau banget hubungan si instrumen dengan variabel yang di-treat. Bukannya memperbaiki, malah bikin OLS tambah parah. Tentu saja masalah lainnya adalah jika ternyata instrumennya punya korelasi dengan Y. Di contoh kita ini tentu saya Y independen terhadap Z, tapi di dunia nyata, sulit banget cari instrumen yang benar-benar independen. Contoh, jika ternyata shock-nya berpengaruh ke sektor finansial, otomatis si-shock ini akan punya pengaruh ke borrowing. Wkkwkwk.

Biasanya yang kita lakukan di paper adalah menunjukkan hasil regresi OLS dan IV, sehingga bisa dilihat pola-nya apakah IV memperbaiki OLS atau tidak. Tentu saja justifikasi dari publikasi lain soal keabsahan IV juga harus ditulis di paper kita wkwk. Di Crawford sendiri, jika anda menggunakan IV, siap-siaplah ditanya-tanyain soal kekuatan instrumennya. Ha ha ha ha!

IV memang ribet. Moga-moga kita tidak harus berurusan dengan IV. wwkwkw. Ok sekian semoga postingannya berguna.